The USA Ultimate Rankings (version 2.0) are used in the College and Club regular seasons to help determine strength wildcard bid allocation throughout the series. The algorithm becomes more accurate later in the season as more valid scores are provided by tournament directors and teams.
The most basic explanation of this rating system is this: for each game a team plays, the team gets a game rating. These ratings are then averaged over all games played by a team.
The next level of complexity is how to compute the points for a given game, and how to average them. The points for a given game is given by the opponent's rating plus or minus (in the case of a win or loss, respectively) some rating differential x.
The number x is a function of the score. Here is the general formula for it:
As an example, suppose team A beats team B 15-11. For a 15-11 game, x = 381. Suppose, further, that team B has a rating of 1010. Then the game rating earned by team A is 1010 381, or 1391.
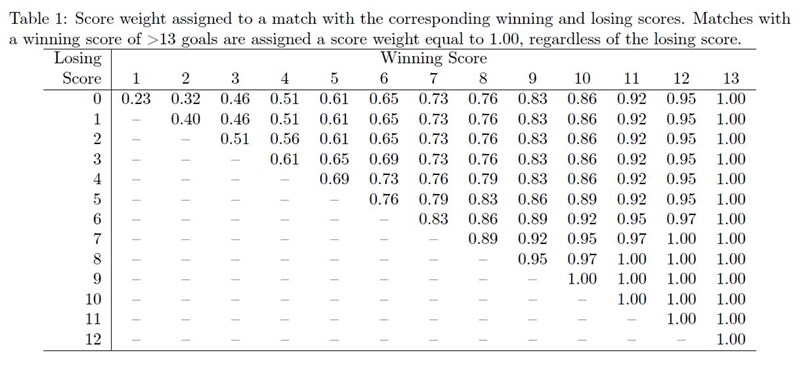
So, suppose team A has played in 4 games, and each individual game rating is 1298, 913, 1410, and 1103. To determine A's overall rating, we take a weighted average of those numbers. The weight of any game is a product of the date weight and the score weight. The date weight depends upon how recently the game was played; games in the first week of the regular season will get a date weight of 0.5, while games in the last week of the season get a date weight of 1.0. Date weights of games in intermediate weeks are interpolated exponentially, so each week's date weight is a fixed multiple of the previous week's date weight. The score weight of a game will be 1.0 if the winning score is at least 13, or if the total score is at least 19. Games with a winning score below 13 and a total score below 19 will get lower score weights. Precisely, the score weight, where W and L denote the winning and losing scores, will be:
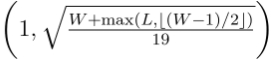
This averaging is done in an iterative process. First, we temporarily set every team's rating to 1000, and compute each individual game rating and take averages. This gives each team a new rating. Then, we re-compute the game ratings and averages, using this new set of ratings, to get yet another set of ratings. We do this thousands of times until the rating for each team has stabilized. If some team does really well, and, after the first iteration their rating goes up 250 points, then, on the second iteration, all teams that have played the first team will go up by a smaller amount, and on the third iteration, all the teams that have played the teams that played the first team will go up by a small amount, and so on.
Finally, if a team is rated more than 600 points higher than its opponent, and wins with a score that is more than twice the losing score plus one, the game is ignored for ratings purposes. However, this is only done if the winning team has at least N other results that are not being ignored, where N=5.
USA Ultimate continues to look to improve its rankings algorithm through consultation with volunteers on the Algorithm Taskforce. The review process is ongoing as we look to enhance the level of competition and goals of USA Ultimate. Any additional changes/alterations to the Algorithm will be communicated as they occur.